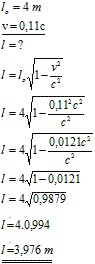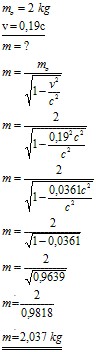MERLIN

•Špeciálna teória relativity - úlohy

•Opakovanie špeciálnej teórie relativity

•Otvorené úlohy A

•Otvorené úlohy B

•Zatvorené úlohy A

•Zatvorené úlohy B

Táto teória vznikla v roku 1905. Jej autorom  je Albert Einstein.

             Špeciálnou sa nazýva preto, lebo vysvetľuje tie fyzikálne javy, pri ktorých je gravitácia zanedbateľná. Podnetom na jej vytvorenie boli problémy s vysvetlením výsledkov niektorých pokusov so svetelnými javmi. Je vybudovaná pomocou myšlienkových pokusov. Vychádza z tvrdení - postulátov:

1. Rýchlosť svetla vo vákuu je vždy a všade rovnaká.
   Predstavme si, že hádžeme loptu po stojačky pred seba. Ak hodíme loptu a bežíme pritom v rovnakom smere, lopta sa bude  pohybovať rýchlejšie. 
   Potom aj rýchlosť svetla z rozsvietenej baterky by mala byť väčšia vtedy, keď s ňou bežíme. Ale žiadny pokus nepotvrdil zmenu rýchlosti svetla, či bol zdroj svetla v pokoji, alebo v  pohybe.
2. Zákony fyziky sú rovnaké, nech sme kdekoľvek. 
   To znamená, že pokus vykonaný v pohybujúcom sa vlaku a na nástupišti bude dávať rovnaké výsledky.  Ak by vlak mal zatemnené okná a pohyboval by sa konštantnou rýchlosťou, potom žiaden pokus nemôže určiť, či je vlak v pohybe, alebo nie je.

Pri svojich pokusoch používal Einstein pojmy:

• Inerciálne vzťažné sústavy - sústavy, ktoré sú navzájom v pokoji, alebo sa pohybujú rovnomerným priamočiatym pohybom.
• Priestoročas (časopriestor)  - štvorrozmerná súradnicová sústava, ktorá má tri geometrické a jednu časovú os.
• Súmiestne udalosti - udalosti,ktoré prebehli na rovnakom mieste.
• Súčasné udalosti - udalosti, ktoré prebehli v rovnakom čase.

Výsledky svojich myšlienkových pokusov zapísal do vzorcov, v ktorých vystupujú fyzikálne veličiny:

1. c = 3. 10⁸ms^-1   - rýchlosť svetla vo vákuu
   
   
2. v  - rýchlosť pohybujúcej sa sústavy
   
   
3. l_o - dĺžka predmetu v sústave nachadzajúcej sa v pokoji
   
   
4. l - dĺžka predmetu v pohybujúcej sa sústave
   
   
5. t_o - časový interval odmeraný v sústave nachadzajúcej sa v pokoji
   
   
6. t - časový interval odmeraný v pohybujúcej sa sústave
   
   
7. m_o - hmotnosť predmetu v sústave nachadzajúcej sa v pokoji
   
   
8. m - hmotnosť predmetu v pohybujúcej sa sústave
   
   
9. E - energia objektu

Špeciálna teória relativity

Elektronická učebnica ŠTR

Stručná formulácia dôsledkov špeciálnej teórie relativity:

1. Absolútny pohyb neexistuje.
   
   
2. Súčasnosť a súmiestnosť javov je relatívna.
   
   
3. Kontrakcia (skracovanie) dĺžky predmetu nastáva pre pozorovateľa v pohybujúcej sa sústave podľa vzťahu
    
    
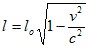
4. Dilatácia (zväčšovanie) časového intervalu nastáva pre pozorovateľa v pohybujúcej sa sústave podľa vzťahu
   
   
    
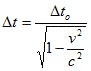
5. Zmena hmotnosti objektu nastáva pre pozorovateľa v pohybujúcej sa sústave podľa vzťahu 
   
   
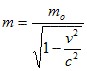
6. Einsteinov vzorec pre celkovú energiu telesa a jeho hmotnosť
   
   
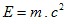
7. Pre javy s objektami, ktoré majú malú hmotnosť a rýchlosť platia zákony klasickej fyziky. Hovoríme, že sú limitným prípadom všeobecnejších relativistických vzťahov. (Teleso má malú hmotnosť vtedy, keď je podstatne menšia ako hmotnosť Slnka. Rýchlosť telesa je malá vtedy, keď je podstatne menšia ako rýchlosť svetla.)

Riešením úloh si ukážeme, aký veľký je vplyv rýchlosti sústavy na veľkosť časového intervalu, na dĺžku predmetu a na zmenu hmotnosti

Úloha 1: V laboratóriu na Zemi pri jadrových reakciách vznikne elementárna častica. Za 5 sekúnd sa rozpadne na iné elementárne častice. Za aký čas sa častica rozpadne v urýchľovači, ak sa v ňom pohybuje rýchlosťou    v = 0,1c?

 Riešenie:
                              

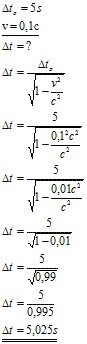
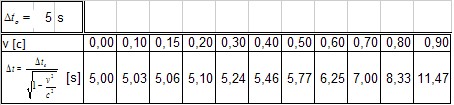
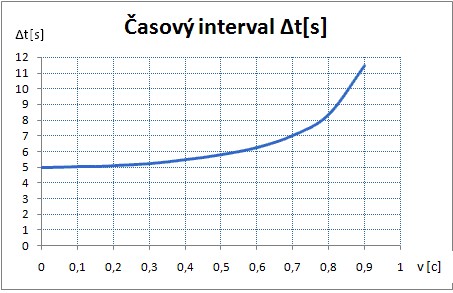
Úloha 2: Zvoľte ďalších 9 hodnôt pre rýchlosť sústavy, vypočítajte veľkosť časového intervalu v pohybujúcej sa sústave pre časový interval v sústave v pokoji rovný 5 s. Zapíšte do tabuľky a vytvorte graf.

Riešenie:

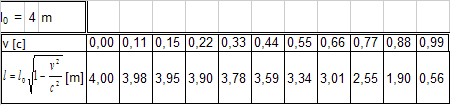
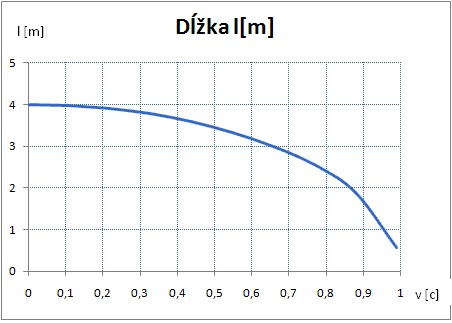
Úloha 3: Vypočítajte veľkosť dĺžky predmetu v sústave pohybujúcej sa rýchlosťou v, ak v sústave v pokoji mala hodnotu 4 m.

Riešenie:  

Úloha 4: Zvoľte ďalších 9 hodnôt pre rýchlosť sústavy, vypočítajte dĺžku predmetu v sústave pohybujúcej sa  rovnomerne priamočiaro v smere dĺžky predmetu, ak dĺžka predmetu je 2 m v sústave, v ktorej je predmet v pokoji. Zapíšte do tabuľky a vytvorte graf.

Riešenie:

Úloha 5: Vypočítajte hmotnosť predmetu v sústave pohybujúcej sa rýchlosťou v, ak v sústave v pokoji mal hmotnosť 2 kg.

Riešenie:

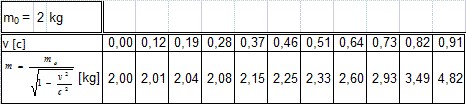
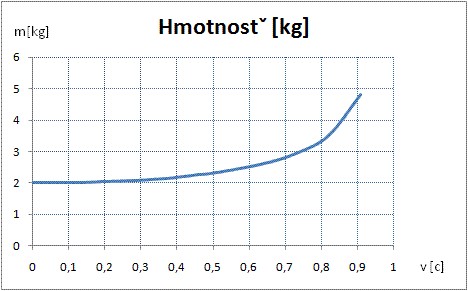
Úloha 6: Zvoľte ďalších 9 hodnôt pre rýchlosť sústavy, vypočítajte hmotnosť objektu v pohybujúcej sa sústave pre hmotnosť v sústave v pokoji rovnú 3 kg.  Zapíšte do tabuľky a vytvorte graf.

Riešenie:

Úloha 7: Aká veľká energia je ekvivalentná hmotnosti 1,1 kg?

Riešenie:

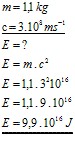
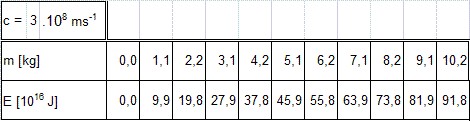
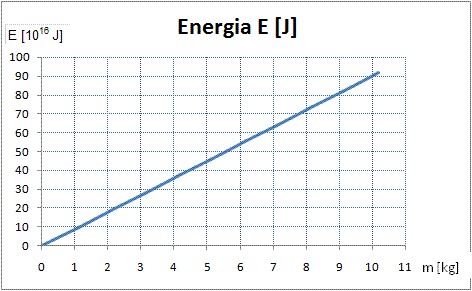
Úloha 8: Zvoľte ďalších 9 hodnôt pre hmotnosť objektu, vypočítajte ekvivalentnú energiu.  Zapíšte do tabuľky a vytvorte graf.

Riešenie:

všeobecná teória relativity